La soustraction au 3eme Harmos 3P représente une pierre angulaire dans les apprentissages fondamentaux des jeunes écoliers. Cette compétence mathématique n’est pas simplement une opération, elle forge le sens des nombres et développe la logique. Notre mission sur Pass Éducation est de fournir un éventail de ressources pédagogiques conçu pour assurer la maîtrise de cette notion cruciale. Les méthodes de soustraction que nous proposons sont adaptées aux besoins spécifiques et au rythme d’apprentissage de chaque enfant, garantissant ainsi une solide compréhension des calculs mathématiques dès le plus jeune âge.
Signes + et – – Exercices corrigés : 3eme Harmos – PDF à imprimer

Exercices corrigés (Nombres et calcul) en 3eme Harmos sur : Signes + et – Consignes pour ces exercices : ❶ Effectue les additions suivantes en dessinant le bon nombre de bonbons puis en écrivant le résultat comme dans l’exemple. ❷ Effectue les additions suivantes en écrivant le résultat. 2 + 3 = __ 1 + 1 = __ 5 + 0 = __ 1 + 3 = __ 2 + 2 = __ 1 + 2 = __ 2 + 1…
Sommes – Différences – Examen Evaluation : 3eme Harmos – PDF à imprimer

Evaluation – Bilan – Sommes – Différences : 3eme Harmos Nombres et calculs – Mathématiques Compétences : Calculer mentalement des sommes et des différences. Consigne pour cette évaluation : Calcule les sommes suivantes. Voir les fiches Télécharger les documents Sommes – Différences : 3eme Harmos – Evaluation – Nombres et calculs – Mathématiques…
Signes + et – – Cours, Leçon : 3eme Harmos – PDF à imprimer

Leçon (Nombres et calcul) en 3eme Harmos sur : Signes + et – Lorsque l’on ajoute des objets, on utilise le signe + (plus), c’est une addition. Lorsque l’on enlève des objets, on utilise le signe – (moins), c’est une soustraction. Voir les fichesTélécharger les documents Leçon : 3eme Harmos période 1_signes + et – R pdf Leçon : 3eme Harmos période 1_signes + et – R rtf…
Signes + et – – Séquence complète : 3eme Harmos – PDF à imprimer

Séquence complète (Nombres et calcul) en 3eme Harmos sur : Signes + et – Lorsque l’on ajoute des objets, on utilise le signe + (plus), c’est une addition. Lorsque l’on enlève des objets, on utilise le signe – (moins), c’est une soustraction. Consignes pour ces exercices : ❶ Effectue les additions suivantes en dessinant le bon nombre de bonbons puis en écrivant le résultat comme dans l’exemple. ❷ Effectue les additions suivantes en écrivant le résultat. 2 + 3 =…
Soustraction en colonnes sans retenue – Exercices : 3eme Harmos – PDF à imprimer

Exercices à imprimer sur la soustraction en colonnes sans retenue pour la 3eme Harmos Exercices de calcul : la soustraction Consignes pour ces exercices : Calcule les soustractions suivantes : Pose et calcule les soustractions suivantes : Voir les fiches Télécharger les documents Soustraction en colonnes sans retenue : 3eme Harmos – Exercices rtf Soustraction en colonnes sans retenue : 3eme Harmos – Exercices pdf…
Technique de la soustraction – Décomptage – Cours, Leçon : 3eme Harmos – PDF à imprimer

Leçon – Technique de la soustraction – Décomptage : 3eme Harmos C10 Calcul : Soustraire un petit nombre à un grand nombre DECOMPTER 12 – 4 = ? → Calculer avec mes doigts et ma tête : Je mets « 12 » dans ma tête. Je lève 4 doigts et je décompte à partir de 12 : « 11, 10, 9, 8 » 12 – 4 = 8 Voir les fichesTélécharger les documents Leçon – Technique de la soustraction – Décomptage : 3eme Harmos…
Soustraction en colonnes avec retenue – Exercices : 3eme Harmos – PDF à imprimer

Exercices à imprimer pour la 3eme Harmos – La soustraction en colonne avec retenue Consignes pour ces exercices : Calcule les soustractions suivantes : Pose et calcule les soustractions suivantes : Voir les fiches Télécharger les documents Soustraction en colonnes avec retenue : 3eme Harmos – Exercices rtf Soustraction en colonnes avec retenue : 3eme Harmos – Exercices pdf…
Ajouter ou retrancher 1 à un nombre – Cours, Leçon : 3eme Harmos – PDF à imprimer

Leçon – Ajouter ou retrancher 1 à un nombre : 3eme Harmos – Calcul C5 Calcul : Ajouter ou retrancher 1 à un nombre → Ajouter 1 à un nombre (+1) Si on ajoute 1 à un nombre donné, on obtient le nombre qui suit : celui qui est juste après sur la bande numérique. Exemple : Calculons 8 + 1. 1 2 3 4 5 6 7 8 9 J’avance d’une case : 8 + 1 = 9. → Retrancher 1 à un nombre (-1) Si on retranche 1…
Surcomptage – Décomptage – Exercices – Calcul : 3eme Harmos – PDF à imprimer

Surcomptage – Décomptage : 3eme Harmos – Exercices – Calcul Exercices de calcul : Surcomptage – décomptage 1 Calcule les additions suivantes en t’aidant si tu veux d’une bande numérique. 12 + 3 = ….. 9 + 2 = ….. 14 + 5 = ….. 10 + 7 = ….. 12 + 5 = ….. 13 + 6 = ….. 15 + 4 = ….. 8 + 6 = ….. 11 + 4 = ….. 2 Complète les suites de…
Soustraction – Cours, Leçon : 3eme Harmos – PDF à imprimer
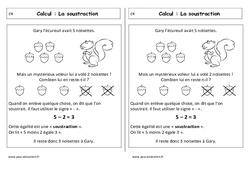
Leçon – Soustraction : 3eme Harmos – Calcul C4 Calcul : La soustraction Gary l’écureuil avait 5 noisettes. Mais un mystérieux voleur lui a volé 2 noisettes ! Combien lui en reste-t-il ? Quand on enlève quelque chose, on dit que l’on soustrait. Il faut utiliser le signe « – ».5 – 2 = 3 Cette égalité est une « soustraction ». On lit « 5 moins 2 égale 3 ». Il reste donc 3 noisettes à Gary. Voir les fichesTélécharger…
Exercices – Soustraction – Calcul : 3eme Harmos – PDF à imprimer

Exercices – Soustraction : 3eme Harmos – Calcul Exercices de calcul : La soustraction 5 – 2 = ….. 1 Dans chaque cas, barre les fruits qu’on ne peut plus manger puis complète la soustraction. 4 – 3 = ….. 4 – 2 = ….. 2 Complète les soustractions suivantes, en t’aidant de dessins. 7 – 1 = ….. 6 – 2 = ….. 3 – 3 = ….. 8 – 4 = ….. 4 – 1 = ….. 9…
Retrancher des dizaines entières – Cours, Leçon : 3eme Harmos – PDF à imprimer
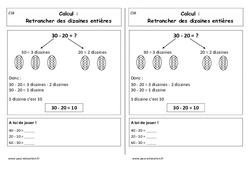
Leçon – Retrancher des dizaines entières : 3eme Harmos C18 Calcul : Retrancher des dizaines entières 30 – 20 = ? 30 = 3 dizaines 20 = 2 dizaines Donc : 30 – 20 = 3 dizaines – 2 dizaines 30 – 20 = 1 dizaine 1 dizaine c’est 10 30 – 20 = 10 A toi de jouer ! 40 – 20 = ….. 20 – 10 = ….. 60 – 30 = ….. Voir les fiches Télécharger les documents Leçon – Retrancher…
Exercices – Ajouter ou retrancher 1 à un nombre – Calcul : 3eme Harmos – PDF à imprimer

Exercices – Ajouter ou retrancher 1 à un nombre – : 3eme Harmos – Calcul Exercices de calcul : Ajouter ou retrancher 1 à un nombre 1 Complète le tableau. -1 avant +1 le nombre après 6 8 2 4 2 Complète les égalités suivantes. 1 + 1 = ….. 3 + 1 = ….. 5 + 1 = ….. 7 + 1 = ….. 3 Complète les égalités suivantes. 7 – 1 = ….. 1 – 1 = ….. 3…
Soustraction posée en colonnes – Cours, Leçon : 3eme Harmos – PDF à imprimer

Leçon – Soustraction posée en colonnes : 3eme Harmos – Calcul C22 Calcul : La soustraction posée en colonnes 86 – 53 = ? 1) Posons d’abord la soustraction avec toujours le plus grand nombre au-dessus. Alignons bien les unités avec les unités et les dizaines avec les dizaines. 8 6 – 5 3 2) Nous allons en premier, soustraire les unités : 6 – 3 = 3. Écrivons alors 3 dans la colonne des unités. 3) Nous allons soustraire ensuite les dizaines : 8 – 5…
Exercices – Retrancher des dizaines entières : 3eme Harmos – PDF à imprimer

Exercices – Retrancher des dizaines entières : 3eme Harmos Exercices de calcul : Retrancher des dizaines entières 1 Complète les égalités suivantes. 40 – 30 = ….. 60 – 20 = ….. 50 – 10 = ….. 70 – 40 = ….. 50 – 50 = ….. 60 – 30 = ….. 2 Calcule le complément. 40 – ….. = 30 60 – ….. = 40 50 – ….. = 10 20 – ….. = 10 70 – ….. = 40…
Exercices – Soustraction posée en colonnes – Calcul : 3eme Harmos – PDF à imprimer

Exercices – Soustraction posée en colonnes : 3eme Harmos – Calcul 1 Calcule les soustractions suivantes. 2 Dans une soustraction, le nombre le plus grand est toujours en premier. Barre les soustractions qui ne respectent pas cette règle. 63 – 53 98 – 82 37 – 58 30 – 41 56 – 89 63 – 12 43 – 12 85 – 91 3 Lis le discours de chaque personnage puis complète. Combien de poissons reste-il à José ? Pose l’opération : Combien de kilomètres lui reste-il à…
Signe + – Exercices – Calculs – Mathématiques : 3eme Harmos
Soustraction en colonnes avec retenue – Révisions : 3eme Harmos – PDF à imprimer

Exercices de calcul sur la soustraction en colonne avec retenue pour la 3eme Harmos Consignes pour ces exercices : Calcule les soustractions suivantes : Pose et calcule les soustractions suivantes : Voir les fiches Télécharger les documents Soustraction en colonnes avec retenue : 3eme Harmos – Révisions à imprimer rtf Soustraction en colonnes avec retenue : 3eme Harmos – Révisions à imprimer pdf…
Soustraction en colonnes sans retenue – Révisions : 3eme Harmos – PDF à imprimer

Exercices à imprimer pour la 3eme Harmos – La soustraction en colonnes sans retenue Exercices de calcul : la soustraction sans retenue Consignes pour ces exercices : Calcule les soustractions suivantes : Pose et calcule les soustractions suivantes : Voir les fiches Télécharger les documents Soustraction en colonnes sans retenue : 3eme Harmos – Révisions rtf Soustraction en colonnes sans retenue : 3eme Harmos – Révisions pdf…
Révisions – Surcomptage – Décomptage – Calcul : 3eme Harmos – PDF à imprimer

Révisions – Surcomptage – Décomptage : 3eme Harmos – Calcul 1 Calcul mental. 2 Calcule les soustractions suivantes en t’aidant si tu veux d’une bande numérique. 14 – 3 = ….. 9 – 5 = ….. 12 – 6 = ….. 10 – 3 = ….. 17 – 3 = ….. 13 – 9 = ….. 19 – 0 = ….. 14 – 4 = ….. 11 – 7 = ….. 3 Compte le nombre d’objets puis calcule. ….. triangles…
Soustraction – Affiche pour la classe – Calcul : 3eme Harmos – PDF à imprimer

Soustraction : 3eme Harmos – Affiche pour la classe – Calcul Calcul : La soustraction Gary l’écureuil avait 5 noisettes. Mais un mystérieux voleur lui a volé 2 noisettes ! Combien lui en reste-t-il ? Quand on enlève quelque chose, on dit que l’on soustrait. Il faut utiliser le signe « – ». 5 – 2 = 3 Cette égalité est une « soustraction ». On lit « 5 moins 2 égale 3 ». Il reste donc 3 noisettes à…
Ajouter ou retrancher 1 à un nombre – Affiche pour la classe – Calcul : 3eme Harmos – PDF à imprimer

Ajouter ou retrancher 1 à un nombre – : 3eme Harmos – Affiche pour la classe – Calcul Calcul : Ajouter ou retrancher 1 à un nombre → Ajouter 1 à un nombre (+1) Si on ajoute 1 à un nombre donné, on obtient le nombre qui suit : celui qui est juste après sur la bande numérique. Exemple : Calculons 8 + 1. 1 2 3 4 5 6 7 8 9 J’avance d’une case : 8 + 1 = 9. → Retrancher 1 à un nombre (-1)…
Révisions – Soustraction – Calcul : 3eme Harmos – PDF à imprimer

Révisions – Soustraction : 3eme Harmos – Calcul 1 Calcul mental. 2 Calcule les soustractions suivantes. 6 – 1 = ….. 9 – 6 = ….. 10 – 7 = ….. 8 – 3 = ….. 2 – 2 = ….. 5 – 4 = ….. 3 Relie les soustractions aux bons résultats. 6 – 1 2 5 – 5 5 10 – 8 4 7 – 3 0 4 Dessine les objets qui ont été volés. Avant le vol Objets…
Révisions – Soustraction posée en colonnes – Calcul : 3eme Harmos – PDF à imprimer

Révisions – Soustraction posée en colonnes : 3eme Harmos – Calcul 1 Calcule les additions suivantes en les posant. 2 Calcul mental. 3 Fais ce qui est demandé. 4 Résous ce problème. Moïse est berger. Hier il avait 89 moutons. Mais le loup a dévoré 66 moutons cette nuit. Combien lui reste-il de moutons ? Voir les fichesTélécharger les documents Révisions – Soustraction posée en colonnes : 3eme Harmos – Calcul rtf Révisions – Soustraction posée en colonnes : 3eme…
Soustraction posée en colonnes – Affiche pour la classe – Calcul : 3eme Harmos – PDF à imprimer

Soustraction posée en colonnes : 3eme Harmos – Affiche pour la classe – Calcul Calcul : La soustraction posée en colonnes 86 – 53 = ? 1) Posons d’abord la soustraction avec toujours le plus grand nombre au-dessus. Alignons bien les unités avec les unités et les dizaines avec les dizaines. 8 6 – 5 3 2) Nous allons en premier, soustraire les unités : 6 – 3 = 3 3) Nous allons soustraire ensuite les dizaines : 8 – 5 = 3 8 6…
Retrancher des dizaines entières – Cours, Leçon : 3eme Harmos – PDF à imprimer
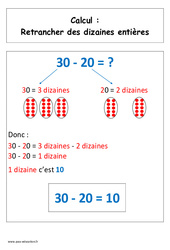
Retrancher des dizaines entières : 3eme Harmos – Affiche pour la classe Calcul : Retrancher des dizaines entières 30 – 20 = ? 30 = 3 dizaines 20 = 2 dizaines Donc : 30 – 20 = 3 dizaines – 2 dizaines 30 – 20 = 1 dizaine 1 dizaine c’est 10 30 – 20 = 10 Voir les fiches Télécharger les documents Retrancher des dizaines entières : 3eme Harmos – Affiche pour la classe rtf Retrancher des dizaines entières : 3eme Harmos…
Technique de la soustraction – Décomptage – Affiche pour la classe : 3eme Harmos – PDF à imprimer

Technique de la soustraction – Décomptage : 3eme Harmos – Affiche pour la classe Calcul : Soustraire un petit nombre à un grand nombre DECOMPTER 12 – 4 = ? → Calculer avec mes doigts et ma tête : Je mets « 12 » dans ma tête. 2) Je lève 4 doigts et je décompte à partir de 12 : « 11, 10, 9, 8 » Voir les fichesTélécharger les documents Technique de la soustraction – Décomptage : 3eme Harmos – Affiche pour…








